Adding, Subtracting, and Multiplying Standard Form Polynomials
We will start with adding and subtracting standard form polynomials, before we move onward to multiplication. For
adding and subtracting polynomials you can only add and subtract like terms. If you don't know what like terms are I
suggest you go back a page to Stand form of Polynomials and review this before going on.
~Adding Polynomials:
Add the polynomials x^(3) + 4x^(2) + 3 and -2x^(2) + x + 6
One way to keep track of what you are doing is to make sure all polynomials are in standard form. It is also
helpful to "fill in" all the missing powers of each polynomial with 0.
These polynomials happen to be in standard form which means we can go ahead and fill in the missing
powers with 0. So that the polynomials become...
x^(3) + 4x^(2) + 0x + 3 As you can see the only numbers changing are the coefficients
+0x^(3) +(-2)x^(2) + x + 6 on the variables. When adding or subtracting polynomials the
x^(3) + 2x^(2) + x + 9 exponents should not change.
Subtract the polynomial x^(3) + 4x^(2) + 3 from -2x^(2) + x + 6
The helpful hints from above still hold true here. The one thing you must pay attention to is which
polynomials is being subtracted from the other. Since subtraction is not commutative the order matters!
0x^(3) - 2x^(2) + x + 6 where as x^(3) + 4x^(2) + 0x + 3
--(x^(3) + 4x^(2) + 0x + 3) --(0x^(3) +(-2)x^(2) + x + 6)
-x^(3) - 6x^(2) +x + 3 =/= x^(3) + 6x^(2) - x - 3
~Multiplying Monomials and Distributive Property:
Multiply the monomials x and x^(2)
(I assume by now you have seen multiplication of variables before and will not explain that in detail here,
however if you need help with this I suggest you go and read up on that before continuing onward with this
page.)
Just like above you can choose to line them up if you wish, or you could remember that multiplication of
variables you just add the exponents.
x * x^(2) = x^(3) another way of writing this would have been x[x^(2)]=x^(3)
The second form of writing the previous example uses the distributive property to multiply the two variables
together, but the distributive property does not only work for monomials...
Now, lets try x multiplied by 2x^(3) + 1 using the distributive property.
x[2x^(3) + 1] = x[2x^(3)] + x[1]= 2x^(4) + x
Next lets try out 2x^(2) times 3x^(5) + 6x^(3) + (3/2)x + (1/2)
2x^(2)[3x^(5) + 6x^(3) + (3/2)x + (1/2)]= 2x^(2)[3x^(5)] + 2x^(2)[6x^(3)] + 2x^(2)[(3/2)x] + 2x^(2)[(1/2)]
=6x^(7) + 12x^(5) + 3x^(3) + x^(2)
~Multiplying Binomials:
Multiply x+1 with 2x+4
Multiplying two binomials together requires the distributive property. You must make sure that each term of
the first polynomial gets multiplied by every term in the second polynomial.
[x+1] [2x+4]= x[2x+4] + 1[2x+4] = x[2x] + 1[2x] + x[4] + 1[4] = 2x^(2) + 2x + 4x + 4 = 2x^(2) + 6x + 4
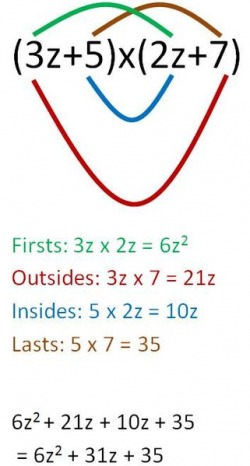
I will now show you the fast way to multiply binomials. It is called the F O I L method. F O I L stands for...
F~ Firsts
O~Outsides
I~Insides
L~Last
Now the F O I L method is still the distributive property (it is just in disguise). You can use the distributive property
on any two polynomials being multiplied, in fact you have too. The key to multiplying polynomials is making sure
you multiply every term in the first polynomial by every term in the second. So, if you have a binomial (2 terms)
multiplied by a trinomial (3 terms) you will have to multiply 6 times in order to multiply the polynomials correctly.
The next page will talk about the finial topic with polynomials and factoring......which is factoring.
on any two polynomials being multiplied, in fact you have too. The key to multiplying polynomials is making sure
you multiply every term in the first polynomial by every term in the second. So, if you have a binomial (2 terms)
multiplied by a trinomial (3 terms) you will have to multiply 6 times in order to multiply the polynomials correctly.
The next page will talk about the finial topic with polynomials and factoring......which is factoring.